Enter the Brachistochrone

• The Problem

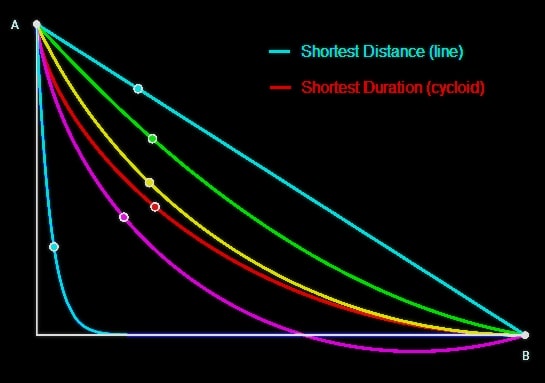
  • Find the shape of the curve down which a bead sliding from rest and accelerated by gravity will slip (without friction) from one point to another in the least time.

• 

• Backstory

  • For hundreds of years mathematicians have been pondering about the simple question above. Galileo famously proposed using a circle's arc, it was not the fastest curve though. The most famous and credited person for answering solving this problem is Johann Bernoulli, who found the solution in 1697. He coined the word "brachistochrone" as the name of the curve he found. Once he discovered the equation for the brachistochrone, he immediately recognized it as a differential equation for the cycloid, which can also be used to describe the brachistochrone.

• 

• 

• Stuck in water

  • Imagine you're in the ocean and you see Bill drowning. You need to save him, but the lifeguard tower is far away; it's displaced 100 yards horizontally and 65 yards vertically. The shoreline recedes 25 yards away from the lifeguard tower. Do you run in a straight line towards the tower or do you escape the water completely and then sprint to the tower?

• Snell's law

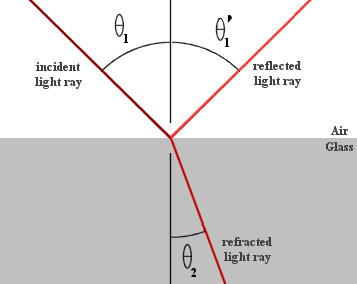
  • Think about how light behaves. It travels slower in water than in air, so by Fermat's principle, it will take the fastest (not necessarily straight) path and is the path you should follow to ensure Billy survives. In the picture on the right, light bends as it enters glass. Snell's law states the sine of theta 1 divided by the speed of light in air is equal to the sine of theta 2 divided by the speed of light in glass. Now how do we tackle the Brachistochrone problem with this?

• 

• Applied to brachistochrones

  • Bernoulli figured that when light refracts it changes direction and the more times it refracts the more the steering of the light would resemble a curve. Using this strategy Bernoulli managed to use Snell's law to draw out an almost continuous curve, one that would allow the fastest movement. This newfound curve would allow circles to roll along the fastest route. The balance between speed and distance was found.

•